一、可数对象
有些题目有一类比较明显的可数对象，有些题有两类比较明显的可数对象。
（一）一类可数对象
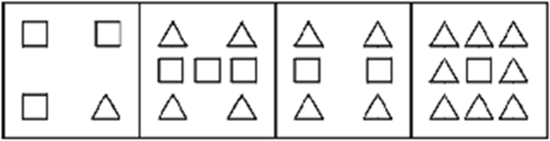
每个图形里面均只有一种元素，即三角形，所以可数对象只有一类。
（二）两类可数对象
结合形状：所有图形一共存在两种元素，即三角形和正方形，所以可数对象有两类。
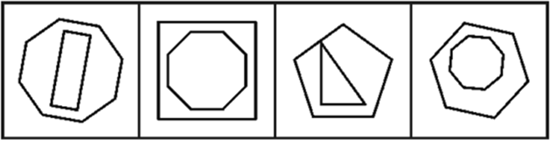
结合结构：所有图形均分为内外两部分，即内部图形和外部图形，所以可数对象有两类。
二、运算思路
（一）一类可数对象
一类可数对象，往往“运算”的规则是三个数中两个做“加/减”运算得到另外一个。
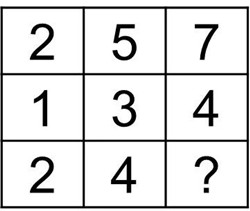
1、横向观察，第1行，前两个数字之和等于第三个数字，即（2+5=7），第2行符合此规律，即（1+3=4），第3行应用规律，前两个数字分别为2和4，相加为6，所以问号处经过运算应该为6。
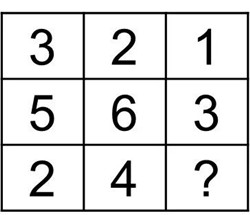
2、纵向观察，第1列，中间数字减去上一个等于下一个数字，即（5-3=2），第2列符合此规律，即（6-2=4），第3列应用规律，中间数字和上一个数字分别为3和1，3-1=2，所以问号处经过运算为2。
3、横向观察，第1行，三个数字之和为10，即（4+4+2=10），第2行符合此规律，即（1+3+6=10），第3行应用规律，前两个数字分别为2和4，所以问号处经过运算应该为4。
（二）两类可数对象
1.各自算
△：2，3，5；1，3，？
○：6，1，5；3，1，？
分析数字规律发现：
三角形：2+3=5；1+3=（4）。
圆：6-1=5；3-1=（2）。
所以，三角形和圆的数字各自存在规律。
2.结合算
①基本运算
组内算的第一种情况是：两类对象间进行“加、减、乘”。
加：
△：2，6，3，4，……；
○：6，2，5，4，……。
纵向观察，三角形的个数加上圆的个数等于8。
减：
△：6，5，3，3，……；
○：4，3，1，1，……。
纵向观察，三角形的个数减去圆的个数等于2。
乘：
△：2，6，3，1，……；
○：6，2，4，12，……。
纵向观察，三角形的个数乘以圆的个数等于12。
②换算
何时算：
a.大部分存在2种元素；
b.组内基本运算无规律；
c.相邻图形间变化一致。
代换公式：
2×（中间图形元素）=（前一个图形元素）+（后一个图形元素）。
三、真题实战
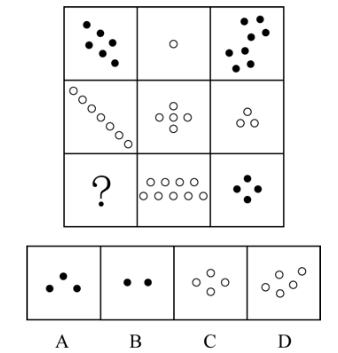
例1（2021联考）
从所给四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：
【解析】
第一步，观察特征。
图形组成均为圆点，优先考虑数量类元素个数。
第二步，九宫格，横向规律较为常见，优先考虑。
第一行圆点个数为6、1、8整体相加为15；第二行圆点个数为7、5、3整体相加为15；第三行后两幅图形圆点个数为9、4，根据前两行元素整体相加为15，所以“？”应为2个圆点，只有B项符合。因此，选择B选项。
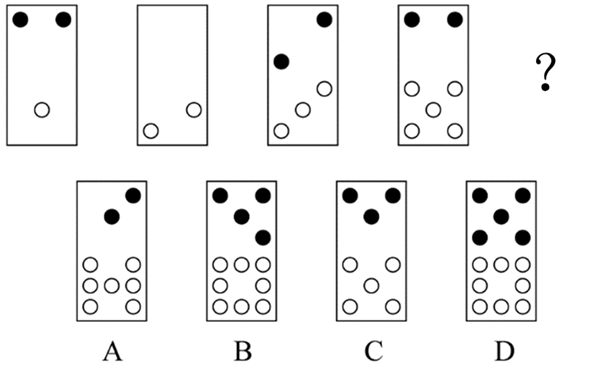
例2（2020河南）
从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：
【解析】
第一步，观察特征。
组成元素不同，优先考虑数量类或属性类。图形中黑点与白点数量特征明显，考虑数黑点与白点的数量。
第二步，一条式，从左到右找规律。
图一和图二中的黑点和白点的数量分别相加等于图三中黑点和白点的数量，图二和图三中的黑点和白点的数量分别相加等于图四中黑点和白点的数量，依此规律，图三和图四中的黑点和白点的数量分别相加等于问号处图形中黑点和白点的数量，只有B项符合。因此，选择B选项。
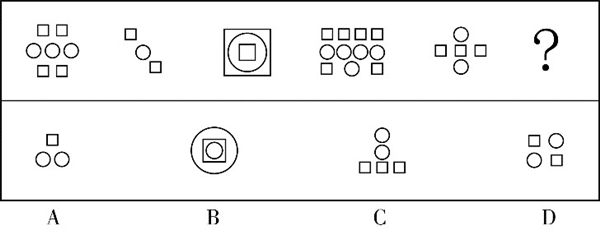
例3（2020江苏）
从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：
【解析】
第一步，观察特征。组成元素不同，考虑数量类。第二步，一条式，从左向右找规律。根据换算规律，图1+图3=2*图2，即3☆+2○=4○+2☆，通过计算可得：1☆=2○，将此关系代入题干，替换为○后从左向右的个数依次为：3、4、5、6、7，所以问号处应选择可以替换成8个○的选项，排除B、D项。题干图形均既有○，又有☆，排除C项，只有A项符合。因此，选择A选项。
例4（2020上海）
下列选项中，符合所给图形的变化规律的是：
【解析】
第一步，观察特征。
题干图形均由两种元素组成，优先考虑两种元素之间的数量关系。
第二步，一条式，从左往右找规律。
观察发现，题干图形中方块个数分别为：4、2、2、6、3；圆形个数分别为：3、1、1、5、2，方块个数-圆形个数都为1，只有C项符合。因此，选择C选项。
【结语】
通过以上的综合分析，相信考生对数量类的考点也有一定的了解和掌握。孙子兵法有云:夫未战而庙算胜者，得算多也；未战而庙算不胜者，得算少也。多算胜，少算不胜，而况于无算呼。希望考生在复习的时候也要多加练习，把方法融会贯通，才能在真正考试时快速“算”出。
更多行测技巧与方法扫码获取
技巧还没掌握？扫码回复“咨询老师”
