一、捆绑法:解决元素“相邻”问题
题目特征:安排时要求某几个元素相邻。
解题步骤:
第一步:先把要求相邻的元素捆绑成一个整体;
第二步:将整体与其他元素进行安排;
第三步:再考虑捆绑的整体内部顺序问题。
例1、6位同事一起去看演出,定了同一排相邻的6个座位,其中小何与小刘必须相邻而坐,则6人选择座位的情况一共有( )种?
A.120
B.240
C.480
D.720
【答案】B。解析:根据题意可知,小何与小刘要相邻,先将小何与小刘捆绑为一个整体并与剩余的4人进行排列,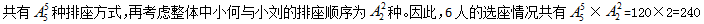 种,故选择B。
种,故选择B。
例2、书桌上有3本相同的数学书,2本相同的外语书,3本其他学科的书,若将这些书排成一列放在书架上,让数学书排在一起,外语书也恰好排在一起的排法共有多少种?
A.120
B.240
C.480
D.1440
【答案】A。解析:题目要求3本数学书相邻、2本外语书也相邻,可将数学书、外语书各自捆绑为一个整体,将这2个整体与3本其他学科的书进行排列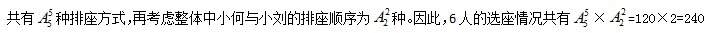 ,选择A。
,选择A。
二、插空法:解决元素“不相邻”问题
题目特征:安排时要求某几个元素不相邻。
解题步骤:
第一步:先安排其他元素;
第二步:再将要求不相邻元素插入其他元素形成的空隙或者两端(若不相邻元素要求不能在两端时,则只能插入中间空隙)。
例3、7人站成一排照相,若要求乙、丙、丁不相邻,则有多少种不同的排法?
A.2400
B.840
C.720
D.1440
【答案】D。解析:根据题意可知,乙、丙、丁为不相邻,使用插空法,先将其它的4个人进行排列,共有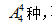 再将乙、丙、丁插入其它4个人形成的三个空隙或两端,
再将乙、丙、丁插入其它4个人形成的三个空隙或两端,
在排列组合题目中,当元素有特殊要求时,怎么选择方法呢?若有元素要求相邻,则用捆绑法;若有元素要求不相邻,则用插空法。我们只要掌握方法,多加练习,此类题目便不再是备考路上的绊脚石。


 更多行测技巧与方法扫码获取
更多行测技巧与方法扫码获取
 行测数量关系考点累积
行测数量关系考点累积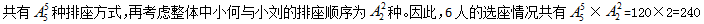 种,故选择B。
种,故选择B。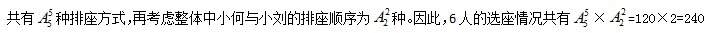 ,选择A。
,选择A。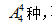 再将乙、丙、丁插入其它4个人形成的三个空隙或两端,
再将乙、丙、丁插入其它4个人形成的三个空隙或两端,
 技巧还没掌握?扫码回复“咨询老师”
技巧还没掌握?扫码回复“咨询老师”

