1.某实心方阵最外层和次外层学生分别组成两个工作小组,分别去完成工作量相等的A、B两项工程,开工8天后,A工程完工,然后两个小组合并,又用了一天,刚好完成了B工程。假设每个学生的工作效率相等,若只安排其余学生去完成与A、B总工作量相等的C工程,需要多少天?
A.16
B.25
C.36
D.48
2.一列火车出发1小时后因故障停车0.5小时,然后以0.75倍的原速度行驶,到达目的地晚点1.5小时;若出发1小时后又行驶120公里再停车0.5小时,然后同样以0.75倍的原速度行驶,则到达目的地晚点1小时。从起点到目的地的距离为多少公里?
A.240
B.300
C.320
D.360
3.有一堆棋子(棋子数大于1),把它们四等分后剩一枚,拿去三份零一枚,将剩下的棋子再四等分后还是剩一枚,再拿去三份零一枚,将剩下的棋子四等分还是剩一枚。问原来至少有多少枚棋子?
A.23
B.37
C.65
D.85
参考与解析:
1.答案:A
解析:
根据“方阵相邻两层人数相差为8”,设方阵最外层人数为x,则次外层人数为x-8。设每个学生一天的工作量为1,依题意有8x=8(x-8)+x+x-8,解得x=36。方阵各层人数依次是36、28、20、12、4,除最外层和次外层还有学生20+12+4=36人,人数与方阵最外层人数相同。C工程的工作量是A工程工作量的2倍,则完成C工程需要8×2=16天。
2.答案:C
解析:
第一次延迟1.5小时,除去因为停车耽误的0.5小时,则因为变速耽误了1小时。变速前后速度比为4∶3,该段路程所用时间比为3∶4。因此第一次变速行驶的距离用原速需要走3小时,从起点到终点以原速行驶需要3+1=4小时。
第二次延迟1小时,因为变速耽误0.5小时,故变速后走了原速走1.5小时的路程。因此120公里即为原速行驶1.5小时走的路程,求得原速为80公里/小时,总路程为80×4=320公里。
3.答案:D
解析:
解析1:根据最后一次将剩下的棋子四等份还剩1枚,那么每等份至少应该是1,即最后剩下的棋子至少应该是4×1+1=5,依次倒推回去,则有(5×4+1)×4+1=85。故正确答案为D。
解析2:根据“把它们四等份后剩一枚”,即棋子的数目除以4余1,排除A,将B、C、D代入,只有85符合题意,即(85-1)/4=21,(21-1)/4=5,(5-1)/4=1,故正确答案为D。
老师点睛:根据题意,设原来至少有a枚棋子,则有(a-1)×1/4×1/4×1/4>1,即a>65,故正确答案为D。


 手机端行测直接刷题
手机端行测直接刷题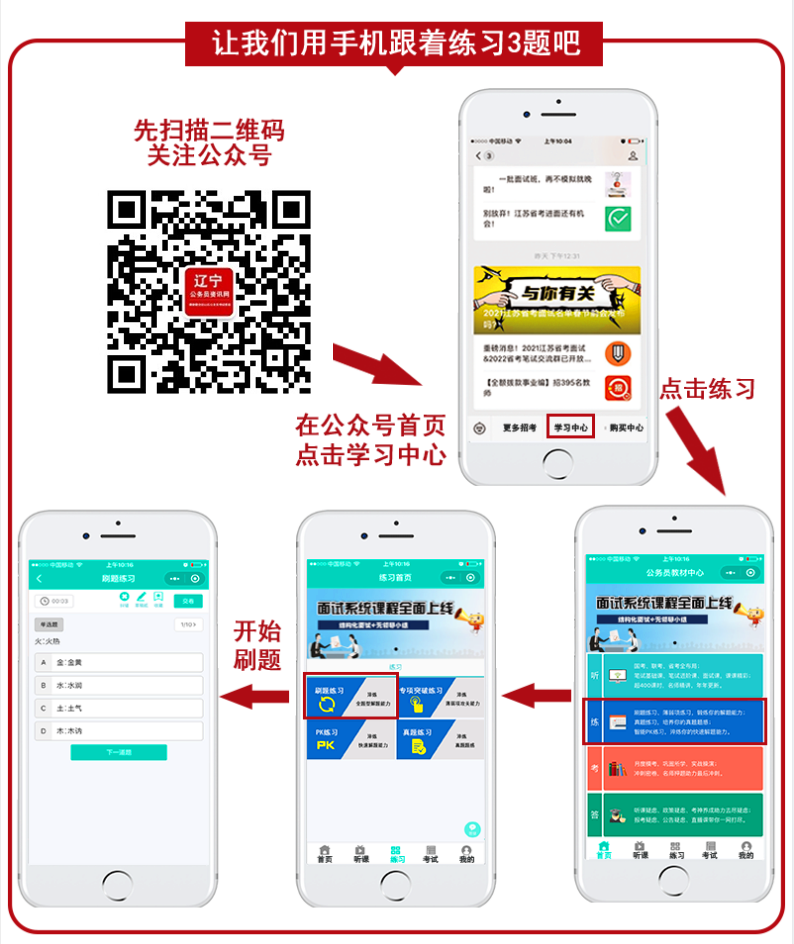
 辽宁公务员考试行测练习
辽宁公务员考试行测练习  刷题不过瘾,想咨询其他?扫码回复“咨询老师”
刷题不过瘾,想咨询其他?扫码回复“咨询老师”

